ベジェ曲線の長さを求める
ベジェ曲線の長さを求める
背景
趣味でアプリを作ってるときにベジェ曲線の長さが必要になりました.ベジェ曲線用のクラスは用意されているものの,長さは自分で計算する必要がありました.色々調べたので記事にまとめることにします.この記事はこのページを参考に執筆しました.
ベジェ曲線とは
CGの分野で曲線はベジェ曲線を用いて表されることが多いです.
下のページではベジェ曲線がわかりやすく紹介されています.解説用のアニメーションが非常にわかりやすいです.
ベジェ曲線の数学的表現
3次ベジェ曲線上の点を媒介変数を用いて
と表すことにします.
このときの始点,制御点1,制御点2,終点をとすれば,
と書けます.
各点の座標,
座標を
,
と書くことにします.構造体のイメージです.
このあとの計算のためにのかっこを展開して
の次数で整理しておきます.係数を
とすれば,
\begin{align}P(t) &= (-P_0+3P_1-3P_2+P_3)t^3 + (3P_0-6P_1+3P_2)t^2 + (-3P_0 + 3P_1)t + (P_0) \\ &= At^3 + Bt^2 + Ct + D \end{align}
となります.
ここで注意してほしいのは,この関数は,
についてそれぞれ成り立っています.すなわち,
ということです.
曲線の長さの求め方
一般に,曲線が媒介変数で
とと表現されているとき,区間
の曲線の長さは
で求められます.
先のベジェ曲線にあてはめれば,
です.
まずはと
を求めるために
を微分してみます.
これを2乗すると,
求めたいベジェ曲線の長さをとすると,
\begin{align} L &= \int_{0}^{1} \sqrt{\left( \frac{dx}{dt} \right)^2 + \left(\frac{dy}{dt} \right)^2} dt. \\ &= \int_{0}^{1} \sqrt{\left( \frac{d}{dt}P(t).x \right)^2 + \left(\frac{d}{dt}P(t).y \right)^2} dt \\ &= \int_{0}^{1} \sqrt{(9(A.x)t^4 +...) + (9(A.y)t^4 + ...)} dt \end{align}
原始関数を求めるのは難しそうです.
であるならば近似解を求める作戦でいきましょう.
この分野には疎いのですが,調べてみたかんじでは数値積分とか数値解析がキーワードのようです.
今回はオイラー法とルンゲクッタ法,シンプソン法を試しました.
ルンゲクッタ法のなかでも4次ルンゲクッタ法と3次ルンゲクッタ法を試しました.
後でわかったことだが,オイラー法とルンゲクッタ法は常微分方程式の近似解を求める手法でした.
Python + matplotlibでベジェ曲線を描く
普段から使い慣れてるPythonでまずはベジェ曲線を描いてみる.
matplotlibの機能だけではベジェ曲線が描けなかったのでモジュールを追加した.
pipでインストールできます.
始点,制御点1,制御点2,終点が
\begin{align*}P_0 &= (0.0,0.0)\\P_1& = (0.5, 3.0)\\ P_2 &= (10.0, -2.0)\\P_3& = (12.0, 4.0)\end{align*}
であるときの3次ベジェ曲線がこちらです.

手法を比較する
手法を比較・評価するときの基準となる"正解"を決めましょう.
自分なりに考えた結果,ベジェ曲線を細かく区切り,その極小区間を直線で近似して三平方の定理で長さを求め,その和を"正解"としました.
シンプソン法(Simpson's rule),オイラー法(Euler method),3次ルンゲクッタ法(3rd-order Runge-Kutta method),4次ルンゲクッタ法(4th-order Runge-Kutta method)を,分割数を10から100まで5ずつ増やして比較してみました.
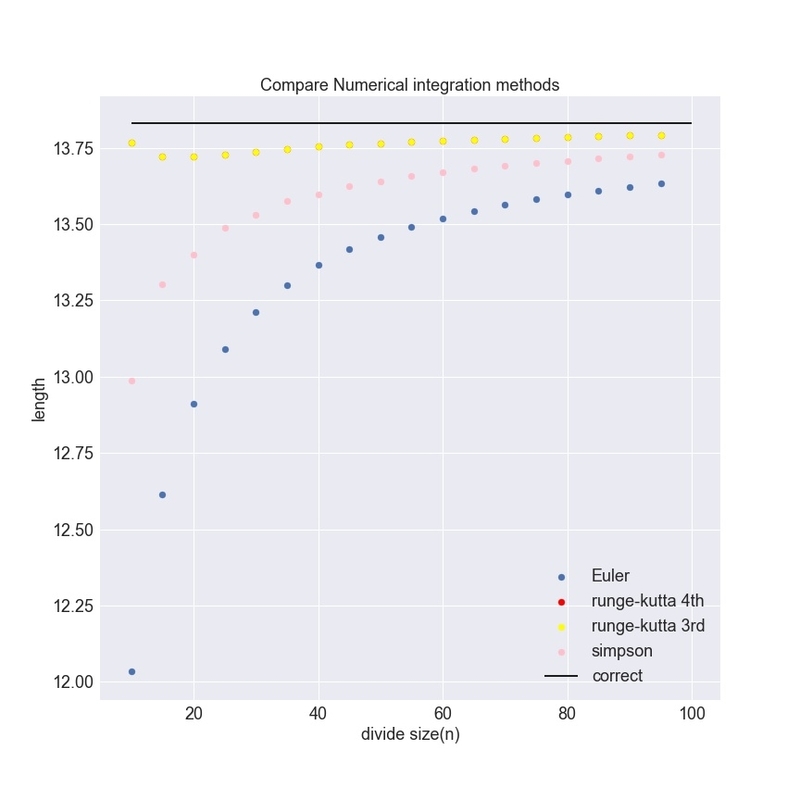
3次のルンゲクッタ法と4次のルンゲクッタ法はかぶってます.
(被積分関数が高々2次であることが関係してそう)
結論
3次のルンゲクッタ法が一番収束も早くて精度がありそうです.
ベジェ曲線クラスが定義されているので,4点を与えれば長さを計算してくれます.
最初の記事だからか気合が入って長くなってしまいました.
お付き合いいただきありがとうございました.